Covariance and contravariance in linear algebra

See also covariance and contravariance on manifolds.

Let $V$ be a vector space, which we will take to have dimension 2 to simplify things. Suppose we have a basis $b1=(u_1,u_2)$ and another one $b_2=(v_1,v_2)$, interpreted as in the basis and change of basis note. We can consider that we have two points of view to describe $V$; and on the other hand we can consider that we have a linear map $T$ which transforms one into the other. That is, $b_2=T\circ b_1$.

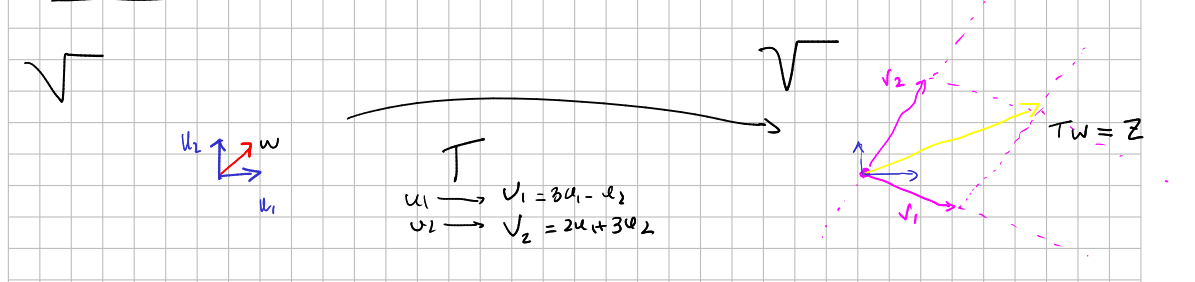
We can call $\tilde{T}_1$ to the matrix of the map $T$ with respect to base $b_1$, that is, the columns are the coordinates of each $v_i$ in base $b_1$

According to basis and change of basis, we have that $\tilde{T}_1=b_1^{-1} \circ T \circ b_1$, and it represents how the transformation is "felt" from the point of view 1. The vector $w=(1,1)$ is transformed into $z=Tw=(5,2)$ in the basis $b_1$, by matrix multiplication with $\begin{pmatrix} 3&2\\ -1 &3\end{pmatrix}$.

On the other hand, since we have two basis, we can wonder about how can we translate from the point of view 1 to the point of view 2. That is, we wonder about the transformation $\mathbb R^2 \to \mathbb R^2$ such that for every $z\in V$

But $A$ is precisely $\tilde{T}_1^{-1}$, since

for every $z\in V$.

In conclusion, the matrix of $T$ from the point of view of $b_1$ is such that its inverse represents the change of point of view from $b_1$ to $b_2$. This means that "changing my point of view of the world" is the opposite of "changing the world." In this sense, it is said that the coordinates of vectors are contravariant.

Now we are going to analyze the coordinates of the covectors, that is, of the elements of the dual space $V^*$

...

... to be completed...

...

and so we obtain the same matrix $\tilde{T}_1$, which justifies saying that the covectors change their coordinates in a covariant manner.

This can be generalized to any kind of transformations on any space, see general covariance and contravariance.

________________________________________

________________________________________

________________________________________

Author of the notes: Antonio J. Pan-Collantes

antonio.pan@uca.es